我对机器学习的兴趣完全是出于好奇。但神经网络在这方面不太吸引我,也许是因为高中生物已经学过很多。
但机器学习里的神经网络——尤其深度神经网络——对我来说是「有用」的。这里我将介绍它在哲学层面给我的一点启发。(其中一些想法未必是对的,仅作记录)
世界是基于通感的
是的,结论就是,世界是基于通感的。我先把结论放在这里。
这种说法会很confusing。因为从唯物主义的角度来说,外部世界是「客观存在」。但当我们说「世界是基于通感的」,指的是:你所认知的世界。
也就是说,在你的心里,在你的概念里,在你的思想里的这个世界。是基于通感而存在的。
让我们从头开始。
首先确保我们知道什么是感知。
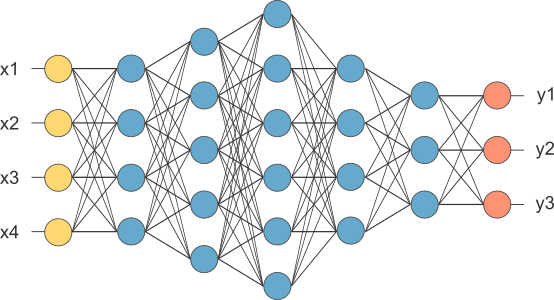
生物学上的每一个神经元,在机器学习里都被用一种类似的运算节点来模拟。这种模拟神经元的运算节点,被称为感知机(perceptron)。无数个感知机交织在一起,搭建出了神经网络——这是我们对生物的模拟。
生物所能获得的感知是什么?——基于各种器官与外部交互时获得的信号:眼睛获取光学信号,耳膜获取声音,皮肤上的感受器获取触觉和温度,位听神经获取平衡感……
这是我们对外界的感知。:器官收集客观的物理化学信息,将其处理成能在生物体内传输的信号。——就目前所知,这种信号类似于一种电信号,即使它们在突触之间也许是利用化学方式传播。
那意识又是什么。
《失控》这本书,有一种很打动我的讨论:意识依赖于感知。
很多人以为把大脑单独拿出来,它里面仍然保存了这个人的意识(缸中之脑)。但KK认为,是你的躯体接收到的这些「感知」赋予了你意识。
1954年,一群加拿大心理学家做了个很有趣的实验。他们搭建了一间避光隔音的实验室,志愿者们呆在这个狭小房间里,头上戴着半透明的防护眼镜,手臂裹着纸板,手上戴着棉手套,耳朵里塞着耳机(里面持续播放低沉的噪音),在床上静躺2-3天。
他们起初还能听到持续的嗡嗡声,不久就融入一片死寂。只看得到暗淡的灰色,与生俱来的五色百感渐渐蒸发殆尽。各种意识挣脱身体的羁绊开始旋转。
半数的受测者都产生了幻觉,声称进入一种“醒时梦”的状态。由于志愿者们的描述太不可靠,有一位研究员以受测者的身份进行了观察:“现实感没了,体像变了,说话困难,尘封的往事历历在目,满脑子性欲,思维迟钝,梦境复杂,以及由忧虑和惊恐引起的目眩神迷”。
在这个与世隔绝的寂静棺材里呆了两天后,几乎所有被试都没有了正常的思维。注意力土崩瓦解,取而代之的是虚幻丛生的白日梦。
这个实验如何解释?我不是在写一本教科书,所以无法给出详细的论证。个人看法:人的神经网络是高度复杂交错构建的。其中不可避免的存在大量的循环。如果没有外部的强刺激来触发某些响应机制,这个网络就会自我运转至一种疯狂状态——所有存在正反馈的环都会无限循环地放大其中信号。你脑海深处产生的一点点小想法,都有可能被强化成一场巨大的无法停止的风暴。
身体是意识乃至生命停泊的港湾,是阻止意识被自酿的风暴吞噬的机器。神经线路天生就有玩火自焚的倾向。如果放任不管,不让它直接连接“外部世界”,聪明的网络就会把自己的构想当作现实。
……
而身体,或者说任何由感觉和催化剂汇集起来的实体,通过加载需要立即处理的紧急事务,打断了神智的胡思乱想!
这个观点对我的启发非常强。Everything you feel is shaping you。你以为是「大脑」在思考,但其实你的所有器官也都在参与「思考」。它们采集的信息不只是被「采集」而已,这些信息是意识运转的基础,它们进入感受器时就已经组成了你的一部分意识。
——你之所以知道自己能控制自己的手指,是因为你驱动它时能感受到相应的触觉、你的眼睛能捕捉到它运动。——若没有这些信息反馈,这一套行动就无法形成闭环——你仅靠想象来决定自己的动作,你的想象就会最终演变为风暴而丧失其应有的意义,因为你的逻辑系统是孤立地运转的。
深度神经网络继续推进我对这个话题的认知,它让我几乎可以从哲学层面来看待人类的「运行」。
『殊途同归』。当初Geoffrey Hinton坚持认为神经网络是才是机器学习的正确方向。他坚持要把自己那篇论文发在Nature上,但在那个年代,所有人都觉得神经网络这个主意已经没救了。他想到其中一个审稿人是Stuart Sutherland,一位很有名的心理学家,就跑去给他解释机器学习里的神经网络以及反向传播算法。这位心理学家 was shocked,因为他发现这群计算机科学家用不同的方法验证了与他们对脑神经科学的研究相似的结论(关于概念如何传播和组织、它们在大脑内的图形结构…)。
这个故事想指出的是,计算机科学家往往从工程的角度来思考如何实现对一些东西的计算,但它们的努力有时同样反映出生物进化的方向。当他们的深度神经网络模型越来越完善的时候,这种模拟,很有可能就是在越来越逼近生物学上的「现实」。
好了,该来具体谈谈机器学习里的神经网络了。如果学习它,你会了解到些什么?
我不列举所有知识。只举对我来说重要的。
至少目前,卷积神经网络在图像识别领域已经获得超出人类的正确率。这证明图像识别应用中的一些技术是「先进」的。
来看:计算机科学家已经在探究深度神经网络工作的「原理」,在图像识别上,输入的图像传给网络第一层时,第一层的所有感知机都只处理简单特征:某些区域的直线、斜线、纯色…
第二层开始,感知机接受前一层传来的处理结果并将它们抽象和组合,这时候它们开始能理解类似:圆形、倒角、长直线……
第三层也许能将信息组织得更抽象,你能看到一些感知机似乎在找鼻子,另一些在找眼睛……(如果你是在训练一个人脸识别的网络)
再往后,后面的层级就会越来越抽象,处理的信息达到人类无法理解的维度。
抱歉我没有找到恰当的配图,我在课上看到过,但当时没有存,现在一时找不到了。总的来说就是:神经网络的浅层如我们预期一样在处理输入信号,将其翻译为一些「有意义」的特征;但随着深度的增加,越靠后的网络层越倾向于把信息往更高维度、更综合的方向抽象,最终形成一个「结果」向外部输出。
它当然跟人脑不像,因为人脑不是这样线性的「输入-输出」模型。但我愿意相信的是:在人脑最重要的核心区域,神经元全部基于高度抽象的“概念”进行运算,你收到的信息,无差别地传入网络(它们也许被预处理过,如视神经已经把光学信号进行了转译),被一套通用的模型处理,输出一些相对稳定的结果(变成你的想法和行动)。
大脑的不同区域看起来是分工的。但它们的功能如此「通用」,以至于你给它输入别的信号它也能慢慢学会处理。为了验证所有大脑神经都是用的同一个「算法」,有人把小鼠的听觉输入切断,然后给负责听觉的大脑皮层接入视觉感官,让动物的auditory cortex学会了看东西……
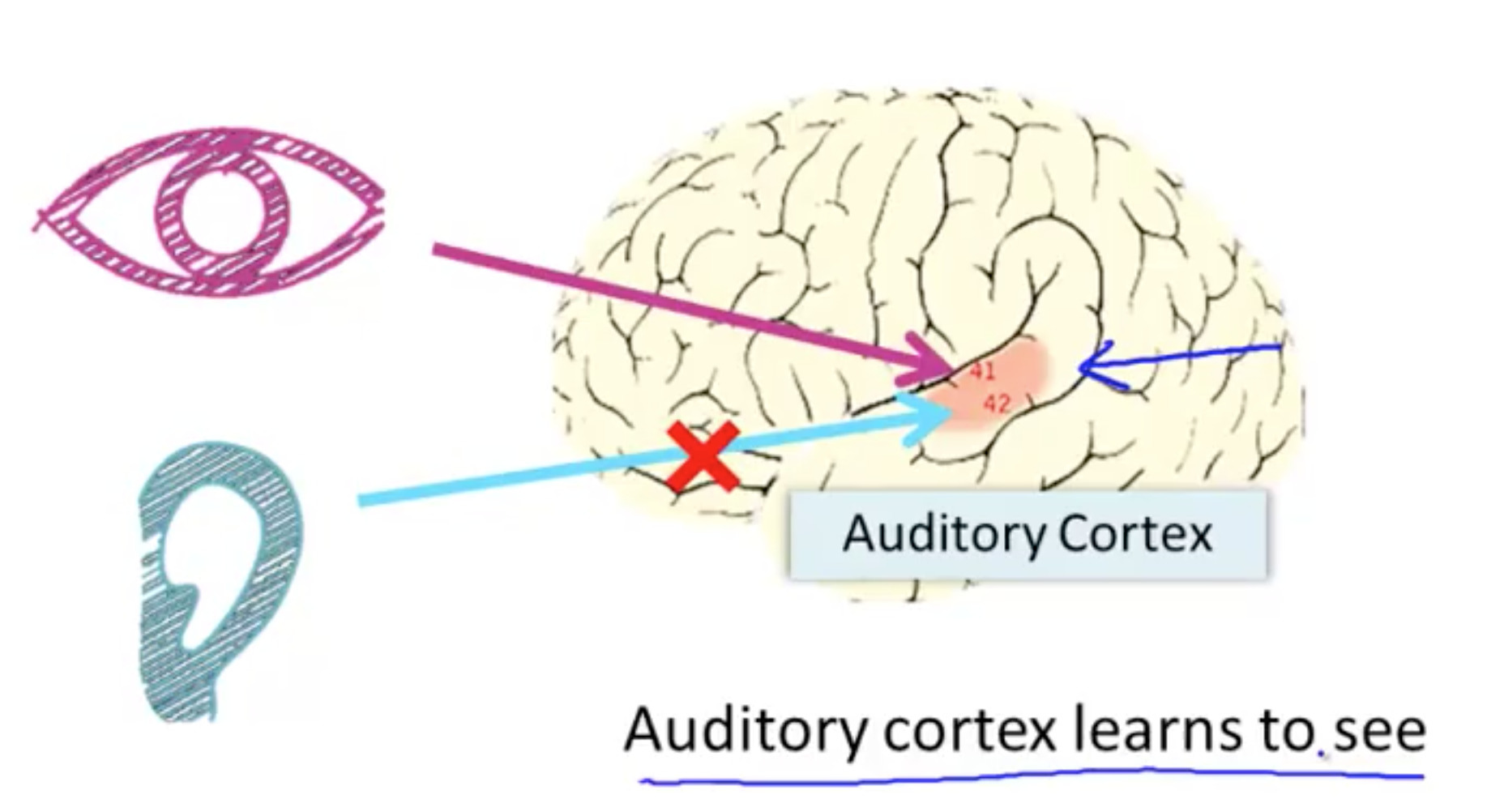
然后他们给盲人做了个头戴式摄像头,采集低清图像转化成灰度图像,将每个像素点的灰度值转换成不同电压传到盲人舌头上。盲人就靠舌头获得了视觉……
这意味着,讯号是可以跨界产生影响的。就像「辣」其实是一种痛觉,但你吃东西的时候会把它判断为这道菜的「味道」。人体是如此复杂的存在,它既是由大脑统控的集中式管理方案,又是器官各自运转的分布式处理系统。你所看到的东西在被视神经收集到的瞬间,视神经已经开始对它做处理。信息层层传递,传到大脑皮层的已经是一些足够抽象的概念——它们甚至已经不必与「视觉」有关。
一束信号如果在传递中串了线,就有可能从「视觉频道」跳到「听觉频道」,当这个概念错误地被听觉大脑皮层处理时,严重时就会让你产生幻听,不严重时…也许你脑内就莫名地产生了一丝忧伤、或者一丝欢愉。
讯号是可以跨界产生影响的,即所谓的“通感”。如果我们认为大脑内有一个核心区域是所有意识交汇的「总成」。就能解释文艺作品中,以下技术有助于推动情绪的原因:环境描写、画面色调、背景音乐……
它们在某种程度上给你传递了“通用”的感受,因为这些不同形式的信号在输入网络的时候都“触动”了一些共同的关键节点。于是你可以从某些颜色、某些旋律、某些文字中感受到近似的悲伤。
刚才提到Geoffrey Hinton和他的反向传播算法,「反向传播算法」指的是,神经网络在进行一次运算之后,会根据输出的结果正确与否接收外界的「惩罚」,这个惩罚会被反向传播回整个路径,使得每个感知机自我修正(下次我就不会再这样了!)。
神经网络是在不断“学习”中变化的。当你被某段感情伤害时,状况就类似于机器学习模型算出了错误的答案,身体的某种机制会去“惩罚”这个错误答案。从而,让整个网络里的每个神经元自我调整。它们产生一种“抑制”,会去回溯在这段感情里你的所有行为和情绪,控制情绪的、控制运动的每个神经元都会根据权重抑制自身。这个“学习”过程让神经网络产生变化:即使跟同一个人发生一段全新的恋情,你的感受和行为也会不一样了,因为你身体的每一个神经元都在学着活得更“正确”。
世界是基于通感的
回到这个结论上来,我认为,从出生起(甚至出生前起),人的感知就在塑造自己(的意识)。气候冷暖在塑造你,你看到的事物在塑造你,你受到的夸奖和委屈也在塑造你。
当你在谈论审美时,你真正指的是什么?
(如果你认同「Everything you feel is shaping you」)也许「审美」只是你从小到大所有感知的加权总和——所有这些感知中让你感到「舒服」的部分,构成了你的审美。
人的大脑是在高度抽象的层面被「训练」的。它不仅仅是学会了一件「具体」的事,而且会跨界产生影响。
就像你学习知识时会用「类比」这种方法。如果所有抽象概念都是在核心区域被处理,那么它学到的经验就可以在毫不相干(却又隐含相同抽象规律)的领域间迁移。即使那些抽象规律并不真正适用于所有领域,若假设人脑的运算能力总是不足的,It’s underfitting,它会用并不普适的经验去处理未知事件就一点也不奇怪了。——就像你生命里的每一个「第一次」尝试。(而且你会在错误尝试后得到「惩罚」,这促使了一次「反向传播」,从而「训练」了你的神经网络,从这个方面来说,你就「学习」了。)
也许你从小生活在局促的空间里,家教很严、做事处世处处受制,长大后想问题的格局也很容易「小器」。
也许你谈恋爱从未失败过,只要努力,想追的女孩就总是能追到手,后来你成了一支基金的经理,潜意识里觉得这种「投资->回报」模型跟追女孩很像,你的投资风格就会异常奔放自信,自以为每次操作都能带来预期中的高收益。
神经网络对我是有用的。我借助它来认识自己。
如果你把人体比做一套高度复杂的神经网络系统,我的建议是:试着了解自己的“网络特性”。——这似乎是与基因有关、取决于成长环境和历程的巨大模型。
然后基于特性去做能够改善网络自身的选择和决定。
以我自己为例:
我认为我的大脑是学习率较高、对错误的punishment超强的类型,同时我会倾向于过早泛化。 这意味着我对未知情况的试探会比较快速和大胆,但一旦得到坏的结果,就会获得很强的负反馈,使之前的所有相关行为都被严重“否定”,这使我很不愿意去做完全没接触过的事情。同时我有很强的倾向去给事物做“抽象”,寻求它们的内在一致性,以尽量总结出可以覆盖更多实例的简单经验。
那我会如何修正自己的选择和决定呢?
——我仍然会鼓励自己去尝试未知,而不是靠既有经验去推断。
——在一些重要的体验发生时,我不会去强化它(让刺激的更刺激),我会去做一些差异化,让正在发生的这件事带上一些不同的特征。这样我在下次遇到类似情况时,就能够因为「差异」而跳出之前的经验,不至于落入一种错误的响应中而丢失宝贵体验。
——不过如果我想活得感性一点的话,在某次重要事件发生时,我会究极强化我的体验,超速飙车、做爱、吸毒一条龙,全方位分泌所有激素去促进神经网络「深刻记住」这一刻。











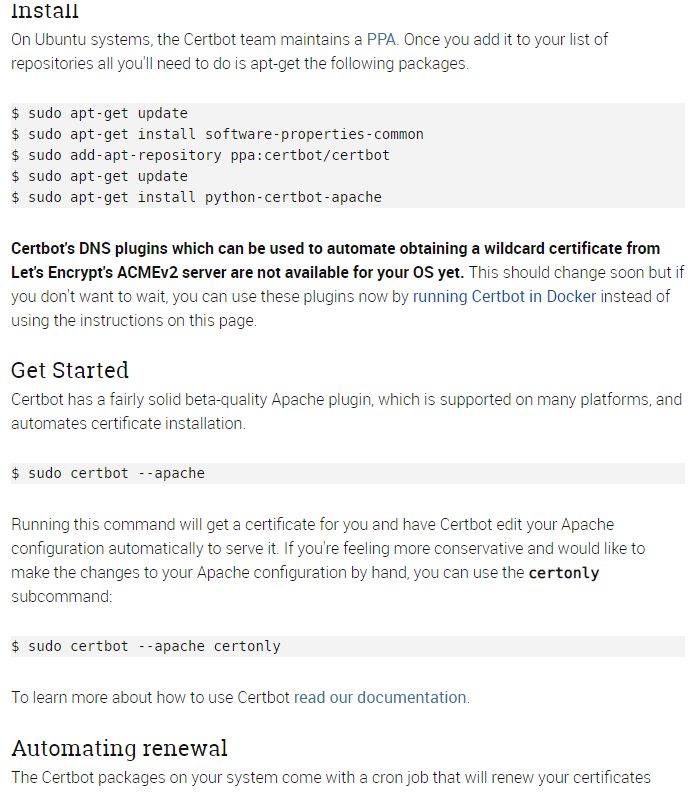 不一定跟我一样,选择你自己的操作系统和服务器软件,certbot 页面上会提供对应的安装方法。
安装后继续按照 certbot 页面的说明 get start ,程序的交互式界面会引导你进行选择和配置。
跟随引导进行操作,完成后网站就被 Let’s Encrypt 提供的 SSL/TLS 证书保护起来了。是不是很有安全感!
不一定跟我一样,选择你自己的操作系统和服务器软件,certbot 页面上会提供对应的安装方法。
安装后继续按照 certbot 页面的说明 get start ,程序的交互式界面会引导你进行选择和配置。
跟随引导进行操作,完成后网站就被 Let’s Encrypt 提供的 SSL/TLS 证书保护起来了。是不是很有安全感!




![Rendered by QuickLaTeX.com \[ \begin{cases} \frac{\partial J}{\partial \theta_1} = \frac{1}{m} (h_\theta(x^1)-y^1) x_1\\ \frac{\partial J}{\partial \theta_2} = \frac{1}{m} (h_\theta(x^2)-y^2) x_2\\ \dots \\ \frac{\partial J}{\partial \theta_n} = \frac{1}{m} (h_\theta(x^n)-y^n) x_n \end{cases} \]](https://www.twisted-meadows.com/wp-content/ql-cache/quicklatex.com-f9b6d356c7a24a2620e66f9856fdf47a_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases} \frac{1}{m} (h_\theta(x^1)-y^1) x_1 = 0\\ \frac{1}{m} (h_\theta(x^2)-y^2) x_2 = 0\\ \dots \\ \frac{1}{m} (h_\theta(x^n)-y^n) x_n = 0 \end{cases} \]](https://www.twisted-meadows.com/wp-content/ql-cache/quicklatex.com-b0229cf18f354e08a97a5d8f64c9482b_l3.png)